GRÁFICOS ABSTRACTOS

“La representación pictórica resulta esencial para el descubrimiento y la rápida comprensión” (John L. Synge)


La Geometría Digital

La geometría digital −un campo dentro de la geometría discreta− maneja conjuntos de puntos discretos digitalizados que representan gráficos de dos o tres dimensiones en el espacio euclídeo. Estos gráficos pueden ser:
Los lenguajes gráficos

En Informática Gráfica (Computer Graphics) se ha dedicado mucho esfuerzo en crear estándares gráficos, con diferentes criterios. Sin embargo, estos estándares constituyen lenguajes aislados, no conectados con un lenguaje general o universal.

Los lenguajes gráficos son lenguajes especializados (como los lenguajes de marcaje, los de gestión de base de datos, etc.), basados en primitivas gráficas específicas (línea, círculo, etc.). Hay lenguajes gráficos tipo vector, raster o ambos. Hay gráficos estáticos y dinámicos. Y hay también lenguajes orientados a interfaz de software: API (Application Program Interface). Los más importantes son:
El algoritmo de Bresenham

El algoritmo de Bresenham sirve para convertir un vector en un conjunto de puntos raster. Determina las celdas de una rejilla bidimensional que deben marcarse (dibujarse) para formar una aproximación a una línea recta entre dos puntos dados. Fue desarrollado por Jack Bresenham en 1962, en IBM, y publicado en 1965 en el IBM Systems Journal [Bresenham, 1965].

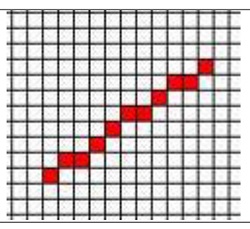
Un ejemplo de vector rasterizado

El algoritmo de Bresenham fue uno de los primeros que se desarrollaron en el campo de la informática gráfica por su simplicidad y efectividad. Solo utiliza suma y resta de números enteros y desplazamiento de bits, operaciones simples que tienen todos los procesadores. No obstante, lo incluyen los procesadores (como hardware o firmware) de las modernas tarjetas gráficas.

Este algoritmo se usa habitualmente para dibujar líneas en una pantalla de ordenador. La pantalla está formada por una matriz bidimensional de pixels direccionables por sus coordenadas (x, y). También se usa en otros dispositivos matriciales, como plotters, impresoras, etc.


El algoritmo en pseudocódigo

Este algoritmo dibuja una serie de pixels entre los puntos (x1, y1) y (x2, y2). Función linea(x1, y1, x2, y2)
   dx = x2−x1
   dy = y2−y1
   error = 0 // error incremental
   p = dy/dx // pendiente de la recta
   y = y1
   Para x = x1 To x2
     draw(x, y) // dibujar pixel en (x, y)
     error = error + p
     Si abs(error) ≥ 0.5 Entonces
       y = y+1
       error = error−1
     Fin Si
   Fin Para
Fin Función

La función dibujar(x, y) sitúa un valor numérico en la celda (x, y), valor que puede ser simplemente 1 (interpretado como “negro”) o bien un número entero asociado a un color (combinación de unos colores básicos) o a una escala de grises. La siguiente es la función generalizada de dibujo de una línea, que tiene en cuenta los posibles valores de dx y dy:

Función lineag(x1, y1, x2, y2)
   dx = x2−x1
   dy = y2−y1
   Caso dx = 0 Entonces
     Para y = y1 To y2
       dibujar(x1, y) // pixel en (x, y)
       Fin Para
   Caso dy = 0 Entonces
     Para x = x1 To x2
       dibujar(x, y1) // pixel en (x, y)
     Fin Para
   Caso dx ≥ dy Entonces
     linea(x1, y1, x2, y2)
   Caso dx < dy Entonces
     linea(x2, y2, x1, y1)
   End Casos
Fin Función


Versión en C

void MidpointLine(int x1,y1,x2,y2)
   {int dx = x2−x1;
   int dy = y2−y1;
   int d = 2*dy−dx;
   int increE = 2*dy;
   int incrNE = 2*(dy−dx);
   x = x1;
   y = y1;
   WritePixel(x, y);
   while (x < x2)
     {if (d<= 0)
       {d+ = incrE;
       x++}
     else
       {d+=incrNE;
       x++;
       y++;}
     WritePixel(x, y);}
     }


Variantes y extensiones del algoritmo de Bresenham

La etiqueta “Bresenham” se usa en una familia completa de algoritmos que extienden o modifican el algoritmo original de Bresenham. Por ejemplo:
MENTAL como Lenguaje Gráfico

MENTAL no solo es capaz de formalizar estructuras geométricas. También es capaz de dibujar sobre una región del espacio abstracto, de tal forma que, con un dispositivo físico, se puede visualizar dicho espacio.


El algoritmo de Bresenham en MENTAL

( linea(x1 y1 x2 y2) =
   ( (d = x2−x1)
   (dy = y2−y1)
   (d = 2*dy – dx)
   (increE = 2*dy)
   (incrNE = 2*(dy−dx))
   (x = x1)
   (y = y1)
   dibujar(x y)
   ⟨(x < x2) →
     (((d = d+incrNE)
     (x = x+1)
     (y = y+1)) ←'
     (d ≤ 0) →
     ((d = d+incrE)
     (x = x+1)))
     dibujar(x y)⟩ )


Las ventajas de MENTAL como lenguaje gráfico

MENTAL se puede utilizar como lenguaje gráfico mediante la utilización de una región dentro del espacio abstracto. El hecho de que el gráfico sea independiente del dispositivo matricial de representación justifica que se pueda calificar a MENTAL de “lenguaje gráfico abstracto”. La utilización de un lenguaje unificado como MENTAL para realizar gráficos proporciona grandes ventajas, ventajas derivadas de las posibilidades del lenguaje, sin más límite que el de la imaginación. La flexibilidad, claridad, simplicidad y creatividad son máximas y van más allá de los estándares gráficos. Por ejemplo: Con MENTAL se pueden crear lenguajes especializados para arquitectura, SIG (sistemas de información geográfica), diseño mecánico, etc.


Algunos ejemplos
  1. Supongamos que queremos que un cierto grupo de puntos sea visible o invisible, dependiendo del valor de una variable. A esos puntos les asignamos el valor ⟨k⟩ (una expresión genérica):


    Haciendo k=0, todos esos puntos serían invisibles. Y haciendo k>0, todos serían visibles. En general, k podría ser un número entero que indicara un color.

  2. Ubicación de un objeto gráfico en un espacio (matriz) gráfico variable:


    Haciendo (E = D), el objeto se ubica en el espacio D.

  3. Ubicación de los puntos de un objeto referidos a un punto determinado del espacio 2D (i0, j0):


    Haciendo (i0=7 j0=9) el objeto mueve según esta posición de referencia.

Adenda

Geometría Computacional

La Geometría Computacional es una rama de la informática dedicada al estudio de los algoritmos que pueden establecerse en términos de geometría. El principal impulso en el desarrollo de la geometría computacional como disciplina fue el progreso en gráficos generados por ordenador (Computer Graphics) y en aplicaciones como CAD/CAM (diseño y fabricación asistidos por ordenador), GIS (sistemas de información geográfica), CAE (ingeniería asistida por ordenador) y diseño de circuitos integrados.

Las dos ramas principales de la geometría computacional son:
  1. La geometría computacional combinatoria, también llamada geometría algorítmica, que trata los objetos geométricos como entidades discretas [Preparata & Shamos, 1988].

  2. La geometría computacional numérica, también llamada geometría de máquina, diseño geométrico asistido por ordenador (CAGD) o modelización geométrica, que trata principalmente de la representación de los objetos del mundo real en formas tratables por los sistemas CAD/CAM. Esta rama se puede considerar un desarrollo ulterior de la geometría descriptiva y a menudo se considera una rama de los gráficos por ordenador o CAD [Forrest, 1971].

Bibliografía